
- Tác giả Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:42.
- Sửa đổi lần cuối 2025-01-22 17:13.
Các SAS Tương tự Định lý phát biểu rằng nếu hai bên trong một Tam giác tỷ lệ với hai bên trong cái khác Tam giác và bao gồm góc trong cả hai đều đồng dư, sau đó hai hình tam giác là tương tự . MỘT giống nhau phép biến hình là một hoặc nhiều phép biến đổi cứng nhắc theo sau bởi một sự giãn nở.
Theo cách này, làm thế nào để bạn chứng minh rằng hai tam giác đồng dạng?
AA (Góc-Góc) Nếu hai các cặp góc tương ứng trong một cặp Hình tam giác đồng dư, sau đó tam giác tương tự . Chúng tôi biết điều này bởi vì nếu hai các cặp góc giống nhau thì cặp góc thứ ba cũng phải bằng nhau. Khi ba cặp góc đều bằng nhau thì ba cặp cạnh đó cũng phải cân xứng.
Tương tự như vậy, làm thế nào bạn có thể biết được các tam giác có đồng dư hay không? Hai tam giác đồng dư nếu chúng có: chính xác ba cạnh giống nhau và. chính xác ba góc bằng nhau.
Có năm cách để tìm xem hai tam giác có đồng dư hay không: SSS, SAS, ASA, AAS và HL.
- SSS (bên, bên, bên)
- SAS (cạnh, góc, cạnh)
- ASA (góc, cạnh, góc)
- AAS (góc, góc, cạnh)
- HL (cạnh huyền, chân)
Người ta cũng có thể hỏi, bạn cần chỉ ra điều gì để chứng minh hai tam giác đồng dạng bằng định lý đồng dạng SAS?
Bạn cần thể hiện điều đó hai các mặt của một Tam giác tỷ lệ với hai các mặt tương ứng của cái khác Tam giác , với các góc tương ứng bao gồm là đồng dư.
Các đường thẳng song song có đồng dư không?
Nếu hai những đường thẳng song song bị cắt bởi một đường ngang, các góc tương ứng là đồng dư . Nếu hai dòng bị cắt bởi một đường ngang và các góc tương ứng là đồng dư , NS các đường thẳng song song . Các góc bên trong ở cùng một phía của đường ngang: Tên là mô tả về "vị trí" của các góc này.
Đề xuất:
Làm thế nào để bạn chứng minh các đường thẳng song song trong chứng minh?

Đầu tiên là nếu các góc tương ứng, các góc nằm trên cùng một góc tại mỗi giao điểm bằng nhau thì các đường thẳng song song. Thứ hai là nếu các góc bên trong thay thế, các góc ở các cạnh đối diện của phương ngang và bên trong các đường thẳng song song, bằng nhau, thì các đường thẳng song song
Làm thế nào để bạn chứng minh tổng các góc bên ngoài của một tam giác là 360?

Góc bên ngoài của một tam giác bằng tổng các góc bên trong đối diện. Để biết thêm về điều này, hãy xem Định lý góc ngoài tam giác. Nếu góc tương đương được lấy ở mỗi đỉnh, thì các góc bên ngoài luôn thêm vào 360 ° Trên thực tế, điều này đúng với bất kỳ đa giác lồi nào, không chỉ tam giác
Làm thế nào để bạn chứng minh rằng các tam giác đồng dạng?

Nếu hai cặp góc tương ứng trong một cặp tam giác đồng dạng thì các tam giác đó đồng dạng. Chúng ta biết điều này bởi vì nếu hai cặp góc bằng nhau thì cặp góc thứ ba cũng phải bằng nhau. Khi ba cặp góc đều bằng nhau thì ba cặp cạnh đó cũng phải tỉ lệ
Làm thế nào để bạn tìm thấy cạnh đối diện của một tam giác bằng cách sử dụng Pitago?
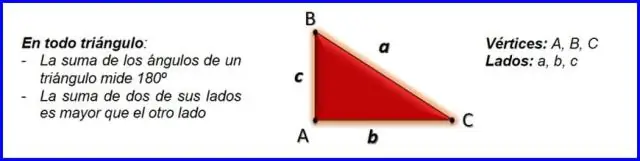
Tam giác vuông và định lý Pitago Định lý Pitago, a2 + b2 = c2, a 2 + b 2 = c 2, có thể được sử dụng để tìm độ dài của bất kỳ cạnh nào của tam giác vuông. Cạnh đối diện với góc vuông được gọi là cạnh huyền (cạnh c trong hình vẽ)
Làm thế nào để bạn chứng minh rằng các góc bằng nhau?

Sau đó, chúng ta đã chứng minh được các định lý chung liên quan đến góc: Các góc đối đỉnh thì bằng nhau. Các góc ngoại tiếp xen kẽ bằng nhau. Các góc nội tiếp xen kẽ bằng nhau. Tổng các góc nội thất trên cùng một phía của mặt cắt ngang là 180 độ
