
- Tác giả Miles Stephen [email protected].
- Public 2023-12-15 23:42.
- Sửa đổi lần cuối 2025-01-22 17:13.
1) Tìm cái đầu tiên phát sinh của f (x). 2) Đặt giá trị x của điểm được chỉ định vào f '(x) để tìm hệ số góc tại x. 3) Cắm giá trị x vào f (x) để tìm tọa độ y của đường tiếp tuyến chỉ trỏ. 4) Kết hợp độ dốc từ bước 2 và điểm từ bước 3 bằng cách sử dụng điểm-độ dốc công thức để tìm phương trình cho đường tiếp tuyến.
Theo quan điểm này, phương trình của một đường tiếp tuyến có phải là đạo hàm không?
Các phát sinh & tuyến tính tiếp tuyến . Các phát sinh của một hàm cung cấp cho chúng ta phạm vi của đường tiếp tuyến vào hàm tại bất kỳ điểm nào trên đồ thị. Điều này có thể được sử dụng để tìm phương trình trong số đó đường tiếp tuyến.
Sau đó, câu hỏi là, làm thế nào để bạn tìm thấy một đạo hàm? Về cơ bản, chúng ta có thể tính đạo hàm của f (x) bằng cách sử dụng định nghĩa ẩn của đạo hàm với các bước sau:
- Tìm f (x + h).
- Đưa f (x + h), f (x) và h vào định nghĩa giới hạn của đạo hàm.
- Đơn giản hóa thương số chênh lệch.
- Lấy giới hạn, khi h gần bằng 0, của thương số đã được đơn giản hóa.
Tương tự, nó được hỏi, làm thế nào để bạn tìm thấy phương trình tiếp tuyến?
Để tìm phương trình của một tiếp tuyến, chúng ta:
- Phân biệt phương trình của đường cong.
- Thay giá trị vào phương trình phân biệt để tìm gradient.
- Thay giá trị vào phương trình ban đầu của đường cong để tìm tọa độ y.
- Thay thế điểm của bạn trên đường thẳng và gradient thành.
Đường tiếp tuyến với đường cong là gì?
Trong hình học, đường tiếp tuyến (hoặc đơn giản đường tiếp tuyến ) đến một máy bay đường cong tại một điểm nhất định là tầm nhìn hàng mà "chỉ cần chạm vào" đường cong tại thời điểm đó. Leibniz định nghĩa nó là hàng thông qua một cặp điểm gần nhau vô hạn trên đường cong . Từ " đường tiếp tuyến "xuất phát từ tiếng Latin tangere," totouch ".
Đề xuất:
Làm thế nào để bạn xác định xem một hàm có một đường tiếp tuyến nằm ngang hay không?

Các đường nằm ngang có hệ số góc bằng không. Do đó, khi đạo hàm bằng 0, đường tiếp tuyến nằm ngang. Để tìm các đường tiếp tuyến ngang, hãy sử dụng đạo hàm của hàm để xác định vị trí các số không và đưa chúng trở lại phương trình ban đầu
Làm thế nào để bạn tìm thấy đạo hàm cấp hai của một hàm trig?
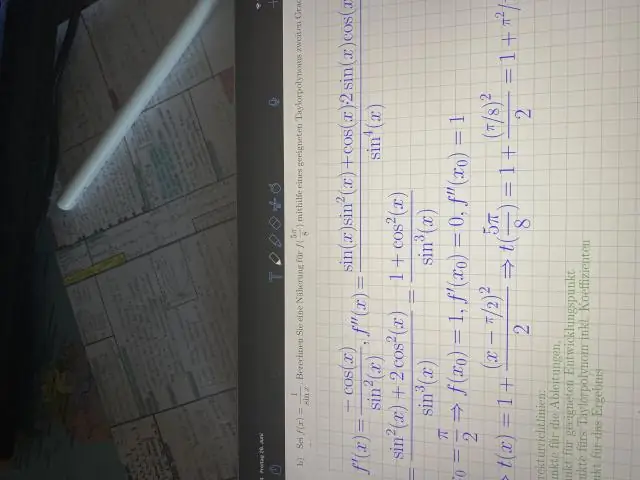
BĂNG HÌNH Chỉ vậy, những gì là đạo hàm của 6 hàm trig? Đạo hàm của các hàm lượng giác. Các hàm lượng giác cơ bản bao gồm 6 hàm sau: tội x), cosin ( cos x), tiếp tuyến (tanx), cotang (cotx), secant (secx) và cosecant (cscx). Tất cả các chức năng này là liên tục và có thể phân biệt trong các lĩnh vực của chúng.
Làm thế nào để bạn tìm thấy phương trình của một đường vuông góc với một điểm?

Đầu tiên, đặt phương trình của đường thẳng cung cấp hệ số góc bằng cách giải cho y. Bạn nhận được y = 2x +5, do đó hệ số góc là –2. Đường vuông góc có độ dốc nghịch đảo, do đó độ dốc của đường chúng ta muốn tìm là 1/2. Cắm điểm đã cho vào hệ thức y = 1 / 2x + b và giải b, ta được b = 6
Làm thế nào để bạn tìm thấy phương trình của một đường thẳng cho trước một điểm và một đường thẳng song song?

Phương trình của đường thẳng ở dạng giao điểm là y = 2x + 5. Hệ số góc của parallelline là như nhau: m = 2. Vậy phương trình của đường thẳng song song là y = 2x + a. Để tìm a, chúng ta sử dụng thực tế là đường thẳng phải đi qua điểm đã cho: 5 = (2) ⋅ (&trừ; 3) + a
Làm thế nào để bạn tìm thấy tiếp tuyến của một góc trên đường tròn đơn vị?

Vòng tròn đơn vị có nhiều góc khác nhau mà mỗi góc có một điểm tương ứng trên đường tròn. Tọa độ của mỗi điểm cho chúng ta một cách để tìm tiếp tuyến của mỗi góc. Tiếp tuyến của một góc bằng tọa độ y chia cho tọa độ x
