Làm thế nào để bạn chứng minh một diều trong hình học tọa độ?

Mục lục:

Đây là hai phương pháp:

Video: Làm thế nào để bạn chứng minh một diều trong hình học tọa độ?

2024 Tác giả: Miles Stephen | [email protected]. Sửa đổi lần cuối: 2023-12-15 23:42

Đây là hai phương pháp:

Nếu hai cặp cạnh liên tiếp rời nhau của một tứ giác là đồng dạng, thì đó là một diều (đảo ngược của diều Định nghĩa).
Nếu một trong các đường chéo của một tứ giác là đường trung trực của tứ giác kia, thì đó là một diều (trò chuyện của một tài sản).

Sau đó, người ta cũng có thể hỏi, đặc điểm của một con diều là gì?

diều các tính chất bao gồm (1) hai cặp cạnh liên tiếp đồng dư, (2) góc không đối đỉnh đồng dư và (3) đường chéo vuông góc. Các tính chất quan trọng khác của đa giác cần làm quen bao gồm tính chất hình thang, tính chất hình bình hành, tính chất hình thoi, tính chất hình chữ nhật và hình vuông.

Cũng biết, một hình chữ nhật có vuông góc không? Như bạn có thể thấy từ các hình bên trái, các đường chéo của một hình chữ nhật không giao nhau theo một góc vuông (chúng không vuông góc ). (Trừ khi hình chữ nhật là một hình vuông.) Và các góc tạo bởi giao tuyến không phải lúc nào cũng có cùng số đo (kích thước). Các góc đối diện ở giữa có cùng kích thước (chúng đồng dư.)

Sau đó, câu hỏi đặt ra là một con diều có vuông góc không?

ĐỊNH NGHĨA: A diều là một tứ giác có bốn cạnh được vẽ sao cho có hai tập hợp các cạnh khác nhau, đồng dư các mặt. LÝ THUYẾT: Nếu một tứ giác là một con diều , các đường chéo là vuông góc . LÝ THUYẾT: Nếu một tứ giác là một con diều , nó có một cặp góc đối diện đồng dư.

Hình chữ nhật có phải là hình bình hành không?

MỘT hình chữ nhật có hai cặp cạnh đối diện song song và bốn góc vuông. Nó cũng là một hình bình hành , vì nó có hai cặp cạnh song song.

Đề xuất:

Làm thế nào để bạn chứng minh các đường thẳng song song trong chứng minh?

Đầu tiên là nếu các góc tương ứng, các góc nằm trên cùng một góc tại mỗi giao điểm bằng nhau thì các đường thẳng song song. Thứ hai là nếu các góc bên trong thay thế, các góc ở các cạnh đối diện của phương ngang và bên trong các đường thẳng song song, bằng nhau, thì các đường thẳng song song

Phép chứng minh nào sử dụng các hình vẽ trên mặt phẳng tọa độ để chứng minh các tính chất hình học?

Một chứng minh sử dụng các hình trên một mặt phẳng tọa độ để chứng minh các tính chất hình học được gọi là lượng giác

Làm thế nào để bạn xây dựng một mặt phẳng tọa độ trong hình học?

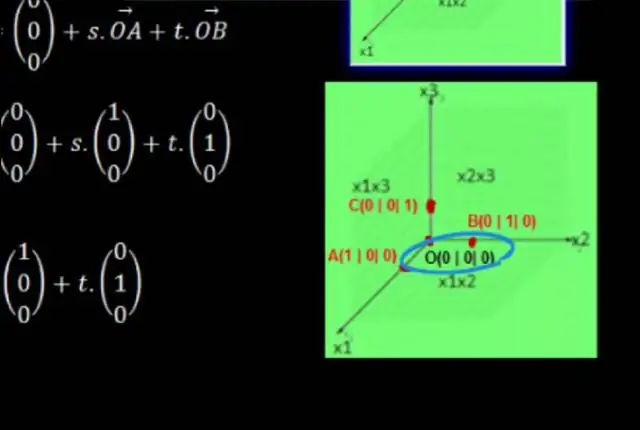
Để tạo một mặt phẳng tọa độ, ta thực hiện theo các bước sau: Vẽ hai trục số vuông góc với nhau, cắt nhau tại điểm 0 trên cả hai đường thẳng. Gắn nhãn đường số ngang là trục x và gắn nhãn đường số dọc là trục y

Làm thế nào để bạn chứng minh một hình bình hành là một hình thoi?

Nếu hai cạnh liên tiếp của một hình bình hành là đồng dư, thì đó là một hình thoi (không phải là đảo ngược của định nghĩa cũng không phải là nghịch đảo của một tính chất). Nếu một trong hai đường chéo của một hình bình hành chia đôi hai góc thì đó là một hình thoi (không phải là đảo ngược của định nghĩa cũng không phải là nghịch đảo của một tính chất)