
- Tác giả Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:42.
- Sửa đổi lần cuối 2025-06-01 05:06.
Chỉ cần nghĩ về một 2x2 ma trận đó là tương tự như nghịch đảo của nó không có các mục đường chéo là 1 hoặc -1. Đường chéo ma trận sẽ làm. Vì vậy, A và nghịch đảo của A là tương tự , vì vậy giá trị đặc trưng của chúng giống nhau. nếu một trong các giá trị riêng của A là n, thì một giá trị riêng của nghịch đảo của nó sẽ là 1 / n.
Cũng được hỏi, một ma trận có tương tự như chuyển vị của nó không?
Hình vuông bất kỳ ma trận trên một lĩnh vực là tương tự như chuyển vị của nó và bất kỳ khu phức hợp hình vuông nào ma trận Là tương tự đến một phức hợp đối xứng ma trận.
Tương tự như vậy, tất cả các ma trận khả nghịch có giống nhau không? Nếu A và B thì tương tự và đảo được , thì A - 1 và B - 1 là tương tự . Bằng chứng. Từ tất cả các NS ma trận là đảo được , chúng ta có thể lấy nghịch đảo của cả hai vế: B - 1 = (P - 1AP) -1 = P - 1A - 1 (P - 1) -1 = P - 1A - 1P, do đó A - 1 và B - 1 là tương tự . Nếu A và B là tương tự , Ak và Bk cũng vậy với bất kỳ k = 1, 2,.
Về điều này, một ma trận có thể tương tự như chính nó?
Đó là, Bất kỳ ma trận Là tương tự như chính nó : I − 1AI = A. Nếu A là tương tự đến B, thì B là tương tự thành A: nếu B = P − 1AP thì A = PBP − 1 = (P − 1) −1BP − 1. Nếu A là tương tự đến B qua B = P − 1AP, và C là tương tự đến B qua C = Q − 1BQ, khi đó A là tương tự thành C: C = Q − 1P − 1APQ = (PQ) −1APQ.
Điều đó có nghĩa là gì nếu các ma trận giống nhau?
Trong đại số tuyến tính, hai n-x-n ma trận A và B được gọi là tương tự nếu tồn tại một n-by-n có thể đảo ngược ma trận P sao cho. Ma trận tương tự biểu diễn cùng một bản đồ tuyến tính dưới hai (có thể) cơ sở khác nhau, với P là sự thay đổi của cơ sở ma trận.
Đề xuất:
Nghịch đảo của một hàm số mũ là gì?
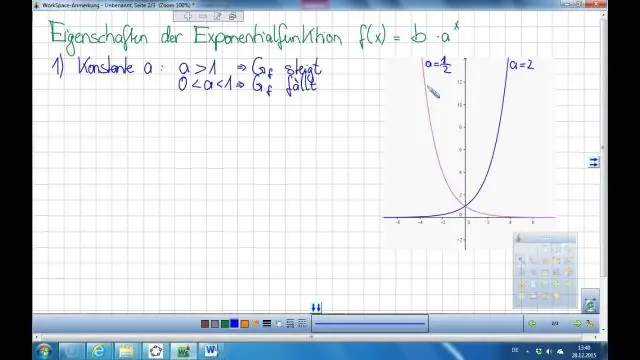
Nghịch biến của hàm số mũ y = ax là x = ay. Hàm logarit y = logax được xác định tương đương với phương trình mũ x = ay
Nghịch đảo của lập phương một số là gì?

Lấy x, lập phương được x3 và chia cho 8 được x3 / 8. X3 / 8 này được gọi là hàm nghịch đảo và được viết là f-1 (x)
Làm thế nào để bạn tìm thấy đối nghịch và nghịch đảo của một số?

Đầu tiên, để đối lập, chúng phải có sự khác biệt. Một số phải là số dương và số còn lại phải là số âm. Thứ hai, để là số có đi có lại, một số phải là phân số lật ngược hoặc đảo ngược của số kia. Ví dụ: phần dưới cùng hoặc phần lật của 3/4 là 4/3
Làm thế nào để bạn tìm thấy nghịch đảo cộng của một ma trận?

Để có được phép cộng nghịch đảo của ma trận đã cho, chúng ta chỉ cần nhân từng phần tử của ma trận với -1. Khi nhân mỗi phần tử của ma trận với -1 thì nó sẽ bằng -A. Do đó, A + (- A) trở thành bằng 0 trong đó 0 là ma trận rỗng. Nó đáp ứng định nghĩa cơ bản của nghịch đảo cộng
Một hòn đảo có phải là một hòn đảo theo nghĩa đen trong một vùng nước?

Đảo là một vùng đất được bao quanh bởi nước. Các lục địa cũng được bao quanh bởi nước, nhưng vì quá lớn nên chúng không được coi là đảo. Những hòn đảo nhỏ này thường được gọi là đảo nhỏ
