Làm thế nào để bạn tìm thấy góc của một khu vực trong biểu đồ hình tròn?

2024 Tác giả: Miles Stephen | [email protected]. Sửa đổi lần cuối: 2023-12-15 23:42

1 câu trả lời

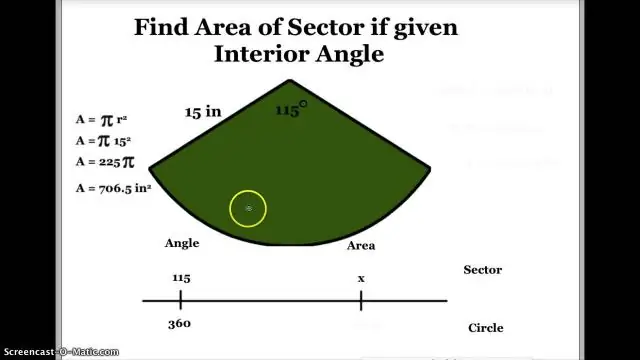
1. Trong bất kỳ khu vực , có 3 phần được xem xét:
2. Chiều dài cung bằng một phần nhỏ của chu vi. khu vực diện tích là một phần nhỏ của toàn bộ diện tích. Các giáo phái là một phần nhỏ của 360 °
3. Nếu khu vực là 20% của biểu đồ tròn , theneachof những phần này là 20% của toàn bộ.
4. 20%×360°
5. 20100×360=72°

Bằng cách này, làm thế nào để bạn tìm thấy độ của một cung của một đường tròn?

Giải thích: Nếu góc trung tâm đo được60 độ , chia tổng 360 độ bên trong khoanh tròn với 60. Nhân giá trị này với số đo của cung tương ứng với tìm thấy tổng chu vi của khoanh tròn . Sử dụng chu vi để tìm thấy theradius, sau đó sử dụng bán kính để tìm thấy khu vực.

Sau đó, câu hỏi đặt ra là, góc trung tâm trong biểu đồ hình tròn là gì? Trong một biểu đồ tròn , các thành phần quan sát khác nhau được đại diện bởi các cung của một vòng tròn và hình tròn đại diện cho tổng các giá trị của tất cả các thành phần. góc trung tâm cho một thành phần được cung cấp bởi: Centralangle cho một thành phần = Giá trị của thành phần Tổng giá trị của tất cả các thành phần × 360 °

Tương tự như vậy, làm thế nào để bạn tìm thấy mức độ của một phần trăm?

Một vòng tròn có 360 độ , vì vậy nếu bạn muốn biểu thị một góc về mặt tỷ lệ phần trăm , chỉ là phép đo hình tam giác (trong độ ) với 360 và nhân với 100. Ngược lại, chia tỷ lệ phần trăm bằng 100 và nhân 360.

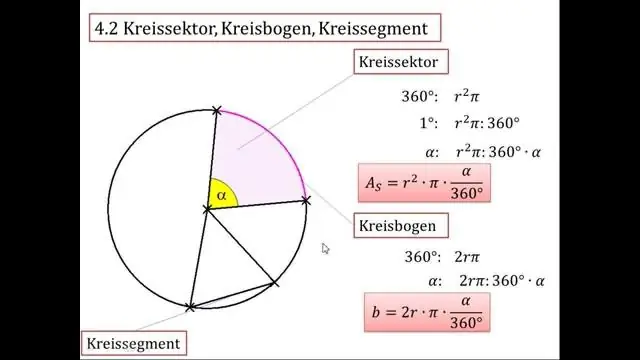
Công thức tìm góc ở tâm là gì?

Công thức cho S = rθ Hình ảnh dưới đây minh họa mối quan hệ giữa bán kính và góc trung tâm tính bằng radian. công thức là S = rθ trong đó s đại diện cho độ dài cung, S = rθ đại diện cho góc trung tâm tính bằng radian và r là độ dài của bán kính.