
- Tác giả Miles Stephen [email protected].
- Public 2023-12-15 23:42.
- Sửa đổi lần cuối 2025-01-22 17:13.
Các tỷ lệ thay đổi tối đa do đó và xảy ra trong phương hướng của gradient, $ abla f (2, 0) = (0, 2) $ và giá trị nhỏ nhất tỉ giá hối đoái đang và xảy ra ở phương hướng ngược lại với gradient, đó là $ - abla f (2, 0) = (0, -2) $. Vì vậy.
Tương tự, người ta có thể hỏi, theo hướng nào thì cơ năng tăng nhanh nhất?
Gradient là phương hướng sau đó chức năng tăng nhanh nhất tại điểm. Giá trị gradient âm là phương hướng sau đó hàm số giảm nhanh chóng nhất tại điểm.
Ngoài ra, tại sao điểm gradient theo hướng tăng tối đa? Các dốc của một hàm nhiều biến có một thành phần cho mỗi phương hướng . Và cũng giống như đạo hàm thông thường, điểm gradient theo hướng tăng mạnh nhất (đây là lý do tại sao: chúng tôi đánh đổi chuyển động trong mỗi phương hướng đủ để tối đa hóa lợi nhuận).
Đơn giản như vậy, làm thế nào để bạn biết con đường nào là dốc nhất?
2x, 2y? = 2? X, y ?; đây là một vectơ song song với vectơ? x, y ?, do đó hướng đi lên dốc nhất trực tiếp cách xa điểm gốc, bắt đầu tại điểm (x, y). Các hướng xuống dốc nhất do đó trực tiếp về phía gốc từ (x, y).
Đạo hàm có hướng cực đại là gì?
Cho một hàm f gồm hai hoặc ba biến và điểm x (theo hai hoặc ba chiều), tối đa giá trị của đạo hàm có hướng tại điểm đó, Duf (x), là | Vf (x) | và nó xảy ra khi u có cùng hướng với vectơ gradient Vf (x).
Đề xuất:
Tại sao thế năng trọng trường lại tăng theo chiều cao?

Vật càng lên cao thì thế năng hấp dẫn của nó càng lớn. Vì hầu hết GPE này được biến đổi thành động năng, vật thể bắt đầu từ càng lên cao càng rơi nhanh khi chạm đất. Vì vậy, sự thay đổi của thế năng trọng trường phụ thuộc vào độ cao mà một vật di chuyển qua
Chiều dài hoặc chiều rộng hoặc chiều cao đầu tiên là gì?
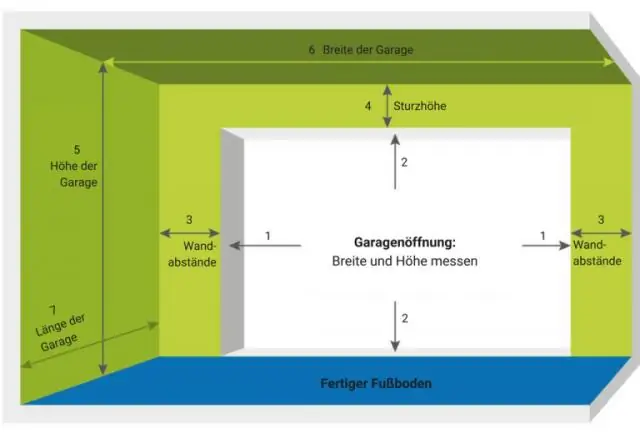
Điều gì đến trước? Tiêu chuẩn ngành của Đồ họa là chiều rộng x chiều cao (width x height). Có nghĩa là khi bạn viết số đo của mình, bạn viết chúng theo quan điểm của bạn, bắt đầu bằng chiều rộng. Đó là quan trọng
Năng lượng của một vật tăng theo chiều cao nào?

Chương 4 Hướng dẫn học tập Câu hỏi Trả lời Nhiệt năng được đo bằng _. joules Năng lượng _ của một vật tăng theo chiều cao của nó. thế năng Động năng của một vật tăng khi _ của nó tăng. tốc độ hoặc khối lượng Năng lượng cơ học là tổng động năng và _ năng lượng trong một hệ thống. tiềm năng
Sự khác nhau giữa chuyển gen theo chiều ngang và chiều dọc?

Chuyển gen theo chiều ngang (HGT) được định nghĩa là việc chuyển vật chất di truyền giữa các tế bào vi khuẩn chưa phân đôi với quá trình phân chia tế bào [1–3]. Ngược lại, di truyền theo chiều dọc là sự truyền vật chất di truyền từ tế bào mẹ sang tế bào con trong quá trình phân bào
Dải Ngân hà quay theo chiều kim đồng hồ hay ngược chiều kim đồng hồ?

Tất cả những gì bạn nhìn thấy bằng mắt thường ngoài Thiên hà Tiên nữ và hai Đám mây Magellan (Bán cầu Nam) đều nằm bên trong Dải Ngân hà. Thời tiết nó quay theo chiều kim đồng hồ hoặc ngược chiều kim đồng hồ tùy thuộc vào cách bạn có thể nhìn vào nó. Trong không gian không có lên hoặc xuống
