
- Tác giả Miles Stephen [email protected].
- Public 2023-12-15 23:42.
- Sửa đổi lần cuối 2025-01-22 17:13.
Các phương pháp vỏ tính thể tích của toàn bộ vật rắn có vòng quay bằng cách lấy tổng thể tích của các vỏ hình trụ mỏng này khi chiều dày Δ x Delta x Δx đi đến 0 0 0 trong giới hạn: V = ∫ d V = ∫ ab 2 π x y dx = ∫ ab 2 π xf (x) dx. V = int dV = int_a ^ b 2 pi x y, dx = int_a ^ b 2 pi x f (x), dx.
Vậy, công thức phương pháp Shell là gì?
Các phương pháp vỏ dựa trên một hình học dễ dàng công thức . Một hình trụ rất mỏng vỏ bọc có thể được tính gần đúng bằng một vật rắn hình chữ nhật rất mỏng. Do đó, khối lượng của vỏ bọc được tính gần đúng bởi thể tích của lăng trụ, là L x W x H = (2 π r) x h x dr = 2πrh dr.
Ngoài ra, công thức phương pháp đĩa là gì? Nói cách khác (các từ ít màu sắc hơn), phương pháp đĩa là quá trình tìm thể tích của một vật bằng cách chia vật đó thành nhiều hình trụ nhỏ / đĩa và sau đó thêm khối lượng của những đĩa cùng nhau. Bán kính của hình trụ được cho bởi một hàm số f (x) và chiều cao là sự thay đổi theo x.
Tương tự như vậy, mọi người hỏi, làm thế nào để bạn sử dụng phương pháp máy giặt trong giải tích?
Cách tìm khối lượng của một hình dạng bằng phương pháp máy giặt
- Xác định vị trí hai đường cong cắt nhau. Vì vậy, vật rắn được đề cập kéo dài một khoảng trên trục x từ 0 đến 1.
- Hình vẽ diện tích mặt cắt ngang của máy giặt.
- Nhân diện tích này với độ dày, dx, để có thể tích của một máy giặt đại diện.
- Cộng các thể tích của vòng đệm từ 0 đến 1 bằng cách tích phân.
Phương pháp vỏ hình trụ là gì?
Các phương pháp vỏ hình trụ . Sử dụng phương pháp vỏ để tính thể tích của vật rắn được tìm ra bằng cách quay vùng giới hạn bởi trục x, đường cong y = x3 và đường thẳng x = 2 về trục y. Đây y = x3 và các giới hạn từ x = 0 đến x = 2.
Đề xuất:
Làm thế nào để bạn sử dụng phương pháp chuyển dời nước để tìm thể tích của một vật không đều?

Đặt đối tượng vào hình trụ chia độ và ghi lại thể tích nước thu được là 'b.' Lấy thể tích của nước trừ đi thể tích của vật cộng với vật. Ví dụ, nếu 'b' là 50 mililit và 'a' là 25 mililit, thì thể tích của vật thể có hình dạng bất thường sẽ là 25 mililit
Làm thế nào để bạn giải quyết các phương trình tuyến tính bằng phương pháp đồ họa?

Giải pháp đồ họa có thể được thực hiện bằng tay (trên giấy kẻ ô vuông) hoặc sử dụng máy tính vẽ đồ thị. Đồ thị của một hệ phương trình tuyến tính cũng đơn giản như đồ thị của hai đường thẳng. Khi các đường được vẽ biểu đồ, nghiệm sẽ là cặp (x, y) có thứ tự nơi hai đường cắt nhau (chéo nhau)
Làm thế nào để bạn giải quyết một vấn đề lập trình tuyến tính bằng phương pháp góc?
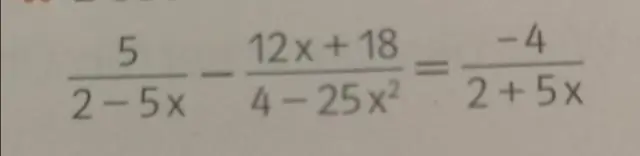
PHƯƠNG PHÁP GÓC GÓC Vẽ đồ thị của tập (vùng) khả thi, S. Tìm tọa độ CHÍNH XÁC của tất cả các đỉnh (điểm góc) của S. Đánh giá hàm mục tiêu, P, tại mỗi đỉnh. Giá trị lớn nhất (nếu nó tồn tại) là giá trị lớn nhất của P tại một đỉnh. Giá trị nhỏ nhất là giá trị nhỏ nhất của P tại một đỉnh
Làm thế nào con người đầu tiên thay đổi cây trồng Các nhà khoa học ngày nay đang sử dụng phương pháp nào để thay đổi cây trồng?

Từ dưa chuột và cà rốt đến gạo trắng và lúa mì, con người chúng ta đã thay đổi gen của hầu hết mọi loại thực phẩm chúng ta ăn. Ngày nay, các nhà khoa học có thể tạo ra một sự thay đổi nhanh chóng bằng cách chọn một gen đơn lẻ có thể dẫn đến một tính trạng mong muốn và chèn trực tiếp gen đó vào nhiễm sắc thể của một sinh vật
Làm thế nào để bạn giải quyết một phương trình hoặc bất phương trình?

Để giải một bất đẳng thức, sử dụng các bước sau: Bước 1 Loại bỏ phân số bằng cách nhân tất cả các số hạng với mẫu số chung nhỏ nhất của tất cả các phân số. Bước 2 Đơn giản hóa bằng cách kết hợp các số hạng giống như trên mỗi vế của bất đẳng thức. Bước 3 Cộng hoặc trừ các đại lượng để thu được ẩn số ở một bên và các số ở bên kia
