Mục lục:
Video: Làm thế nào để cấp tiến hoạt động trong toán học?
2024 Tác giả: Miles Stephen | [email protected]. Sửa đổi lần cuối: 2023-12-15 23:42
Trong toán học , Một căn bản biểu thức được định nghĩa dưới dạng bất kỳ biểu thức nào có chứa căn bản (√) ký hiệu. Nhiều người nhầm lẫn gọi đây là ký hiệu 'căn bậc hai' và nhiều lần nó được dùng để xác định căn bậc hai của một số, ví dụ, 3√ (8) có nghĩa là tìm căn bậc hai của 8.
Đối với điều này, một phương trình cấp tiến là gì?
MỘT phương trình căn bản là một phương trình trong biến whicha nằm dưới căn bản . Để giải quyết một radicalequation : Cô lập căn bản biểu thức liên quan đến biến. Nếu nhiều hơn một căn bản biểu thức liên quan đến biến, sau đó cô lập một trong số chúng. Nâng cao cả hai mặt của phương trình vào chỉ mục của căn bản.
Tương tự, chỉ số làm gì trong một căn nguyên? Và con số nhỏ đó ở bên trái của căn bản dấu hiệu chính xác là những gì có nghĩa là " mục lục sau đó căn bản . "Nói cách khác, mục lục là con số cho bạn biết bạn phải lấy root nào.
Sau đó, làm thế nào để bạn đơn giản hóa các gốc?
Làm thế nào để đơn giản hóa các bước của bộ trao đổi
- Tìm hình vuông hoàn hảo lớn nhất là nhân tử của hình vuông.
- Viết lại căn dưới dạng tích của căn bậc hai của 4 (được tìm thấy ở bước cuối cùng) và hệ số phù hợp của nó (2)
- Đơn giản hóa.
- Tìm hình vuông hoàn hảo lớn nhất là một thừa số của theradicand (giống như trước đó)
Các gốc trong các ví dụ toán học là gì?
Một biểu thức sử dụng một căn, chẳng hạn như căn bậc hai, căn bậc hai. Xem định nghĩa của root. Số lần radicandis nhân với chính nó. 2 có nghĩa là căn bậc hai, 3 có nghĩa là khối lập phương.
Đề xuất:
Làm thế nào để các hàm hoạt động trong toán học?
Trong toán học, một hàm là một quan hệ giữa các tập hợp liên kết với mọi phần tử của tập hợp đầu tiên đúng với một phần tử của tập hợp thứ hai. Ví dụ điển hình là các hàm từ số nguyên sang số nguyên hoặc từ số thực sang số thực. Ví dụ, vị trí của một hành tinh là một hàm của thời gian
Làm thế nào để bạn tính toán hoạt động của nước trong thực phẩm?
Hoạt độ nước bằng độ ẩm tương đối cân bằng chia cho 100: (a w = ERH / 100) trong đó ERH là độ ẩm tương đối cân bằng (%). Cảm biến độ ẩm tương đối có rất nhiều loại cho mục đích này, bao gồm cả ẩm kế điện, tế bào điểm sương, psychrometers và các loại khác
Làm thế nào để các góc phần tư hoạt động trong toán học?
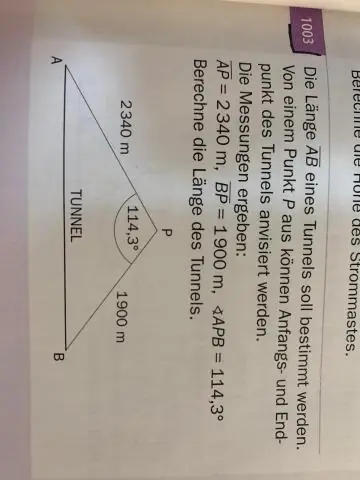
Các trục của một hệ Descartes hai chiều chia mặt phẳng thành bốn vùng vô hạn, được gọi là các góc phần tư, mỗi vùng được giới hạn bởi hai nửa trục. Khi các trục được vẽ theo thông lệ toán học, việc đánh số sẽ đi ngược chiều kim đồng hồ bắt đầu từ góc phần tư phía trên bên phải ('đông bắc')
Làm thế nào con người đầu tiên thay đổi cây trồng Các nhà khoa học ngày nay đang sử dụng phương pháp nào để thay đổi cây trồng?
Từ dưa chuột và cà rốt đến gạo trắng và lúa mì, con người chúng ta đã thay đổi gen của hầu hết mọi loại thực phẩm chúng ta ăn. Ngày nay, các nhà khoa học có thể tạo ra một sự thay đổi nhanh chóng bằng cách chọn một gen đơn lẻ có thể dẫn đến một tính trạng mong muốn và chèn trực tiếp gen đó vào nhiễm sắc thể của một sinh vật
Tiến hóa sinh học hay tiến hóa hóa học đầu tiên ra đời?
Tất cả các dạng sống được cho là đã tiến hóa từ các sinh vật nhân sơ ban đầu, có thể là 3,5-4,0 tỷ năm trước. Các điều kiện hóa học và vật lý của Trái đất nguyên thủy được viện dẫn để giải thích nguồn gốc của sự sống, vốn có trước quá trình tiến hóa hóa học của các hóa chất hữu cơ